FEM04-里玆法 (Ritz Method)

简介

在“FEM02-连续系统的微分方程”和“FEM03-变分法与最小势能原理”中，我们完成了工程分析的第一步：用数学模型来描述实际问题，建立了问题的控制方程。下一步，我们将对数学模型进行求解，本文介绍采用里玆法近似求解微分方程的过程。

里玆法概述

根据变分法，系统的总势能Π，是关于状态变量u的泛函；u是未知的场函数，它的解一定使得总势能Π最小，即Π的变分δΠ=0（最小势能原理）。这似乎给我们提供了一个求解的思路：只要我们从众多的函数中，找到一个函数u使δΠ=0，那么u就是问题的解。但不幸的是：我们不可能把所有可能的函数罗列出来，从中找到满足δΠ=0的解。因为，可能的函数有无限多个而且毫无规律，从中找到答案可能比“大海捞针”更加困难。

里玆法的提出，让变分法的求解思路得以实现。里玆法的核心思想是：放弃寻找准确解，而从一簇特定的函数中找到最接近准确解的近似解。这一簇“特定的函数”通常称为“近似函数”或者“试函数”（trial functions）。

The key to rendering this problem tractable is the method of Ritz. The method of Ritz, tells us to forego looking for an exact solution and to look instead for an approximate solution from within a (well selected) finite set of functions.

采用里玆法求近似解时，我们可以自由地选择一类便于处理的函数（通常是多项式函数）作为试函数，然后从这些试函数中找到最佳的近似解。

将试函数记作ū，假设其形式为：

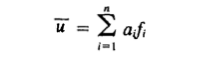
其中，f_i是线性无关的基函数，a_i是待定系数。选择合适的基函数，使试函数满足本质边界条件。（无需满足自然边界条件，因为自然边界条件隐含在泛函总势能中。）

现在，原问题变为：找到一组合适的系数a_i，代入试函数ū，使得总势能Π取最小值。用数学语言来描述，即：

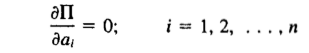
对于a₁~a_n这n个系数，分别求偏导=0，可以得到n个代数方程。联立方程组，可以求出这些系数a_i；代入试函数ū，即可得到近似解。

例题

针对“FEM01-离散系统的求解方法”中的例1.2，采用里玆法计算位移和应力。

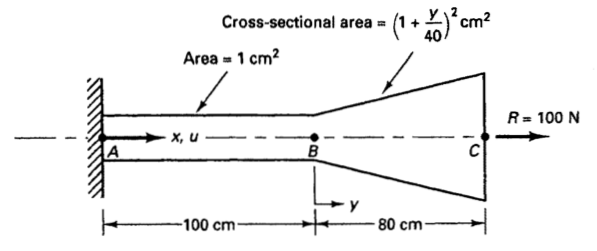
结构的总势能为：

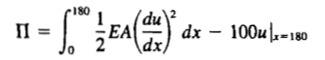
分别采用一次函数和二次函数作为里玆法的试函数，进行求解。

试函数为分段一次函数：以下试函数满足本质边界条件u(x=0)=0；其中，u_B和u_C分别是B、C两点的位移，也是里玆法中需要求解的待定系数。

首先，写出试函数对应的总势能Π。

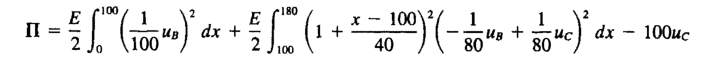
然后，根据∂Π/∂a_i=0，推导出关于u_B和u_C的代数方程组。

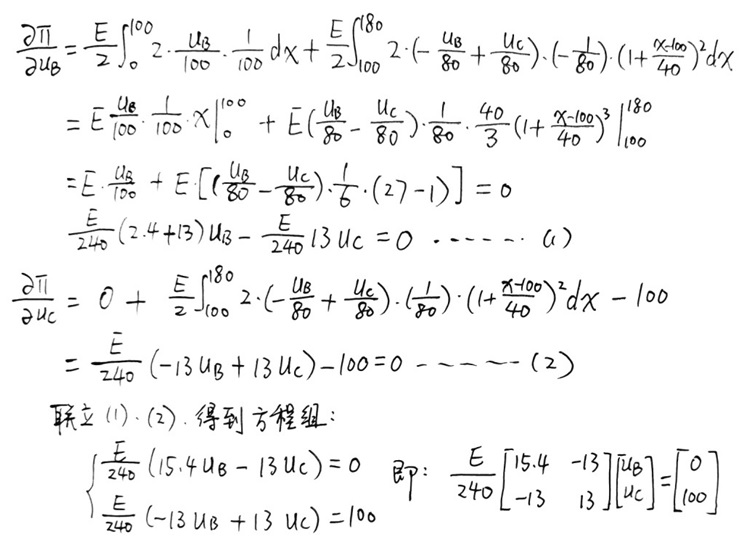
最后，解方程组得到u_B、u_C，代入试函数得到近似解。

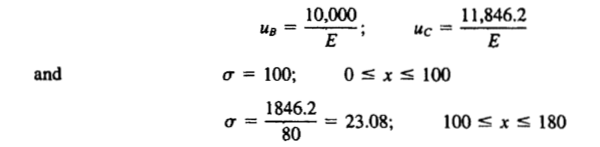
试函数为二次函数：以下试函数满足本质边界条件u(x=0)=0；其中，a₁、a₂是里玆法中需要求解的待定系数。

以上分别采用两种不同阶次的多项式函数作为试函数，运用里玆法求解得到了近似解。近似解与准确解的对比如下图。

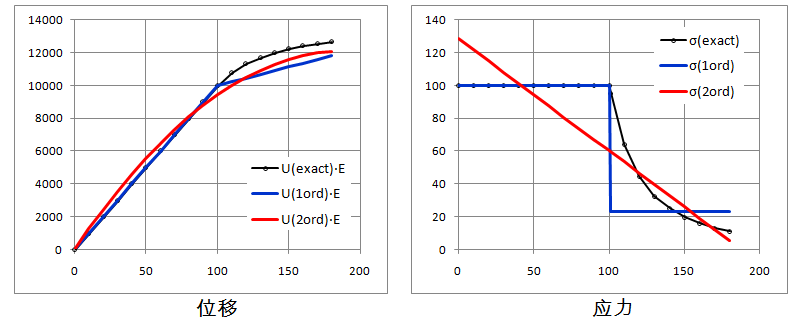
总结

里玆法用试函数近似代替未知变量的场函数，从一簇预先指定的试函数中，找到最佳的近似解。这种采用试函数求近似解的思想，是有限元法的基础。试函数的选择，比较灵活，为了便于计算，一般采用多项式函数作为试函数。试函数既可以在全域上定义，也可以在分段的子域上分别定义。

如果控制方程中状态变量的最高阶导数的阶次是2m，里玆法的试函数只需m阶可导，而且只需满足本质边界条件，不必满足自然边界条件。当然，选择试函数时，可以选择m阶可导的函数，也可以选择比m阶更高阶可导的函数。

Reference:

• Finite Element Procedures by Klaus-Jürgen Bathe 轩建平 译
• A First Course in Finite Elements by Jacob Fish & Ted Belytschko